matrix(data = c(20, 30, 15, 7), nrow = 2, ncol = 2, byrow = T) [,1] [,2]
[1,] 20 30
[2,] 15 7Una asociación es una relación que puede o no conllevar causalidad; es decir que dos (o más) variables pueden estar asociadas o relacionadas independientemente de si una es causa de la otra. De acuerdo a lo anterior podemos establecer las siguientes posibilidades de correlación entre A y B:
Correlación causal: A es causa de B.
Correlación no causal: C es causa de A y B
Correlación independiente de la causa: C es causa de A y D es causa de B
Una estadística que mida la magnitud de la asociación entre dos variables se denomina medida de asociación si la relación es simétrica, o sea que no hay distinción entre una variable de clasificación (variable explicativa o independiente) y una variable de respuesta (variable dependiente); se denomina medida de tamaño del efecto si la relación es asimérica, es decir, una de las variables cumple el papel de variable respuesta. (Díaz Monroy and Morales Rivera 2009)
Ejemplos de estadísticos que miden el tamaño del efecto son:
RP: Razón de prevalencia, usado en estudios Transversales Analíticos.
RR: Riesgo relativo, usado en estudios de Cohorte.
OR: ODDS Ratio (ó RM = Razón de momios), usado en estudios de Casos y Controles.
Coeficiente de contingencia.
Coeficiente Phi.
V de Cramer.
Para estudios de Casos y Controles y estudios de Cohorte se debe seleccionar un test estadístico para evaluar la significancia de la asociación, mientras que en los estudios transversales no es necesario dado que son más bien descriptivos. A continuación se muestra una guía para seleccionar el test estadístico en los estudios que corresponda.
Los estudios observacionales se utilizan para identificar los factores de riesgo y estimar los efectos cuantitativos de las diversas causas que contribuyen a la ocurrencia de la enfermedad.
Las investigaciones se basan en el análisis de la ocurrencia de enfermedades naturales en las poblaciones comparando grupos de individuos con respecto a la aparición de la enfermedad y exposición a factores de riesgos hipotéticos.
Los estudios observacionales difieren de los estudios experimentales; en el primer caso, el investigador no es libre de asignar factores aleatoriamente a los individuos, mientras que en estos últimos el investigador es libre de asignar factores a los individuos al azar. (Thrusfield 2008)
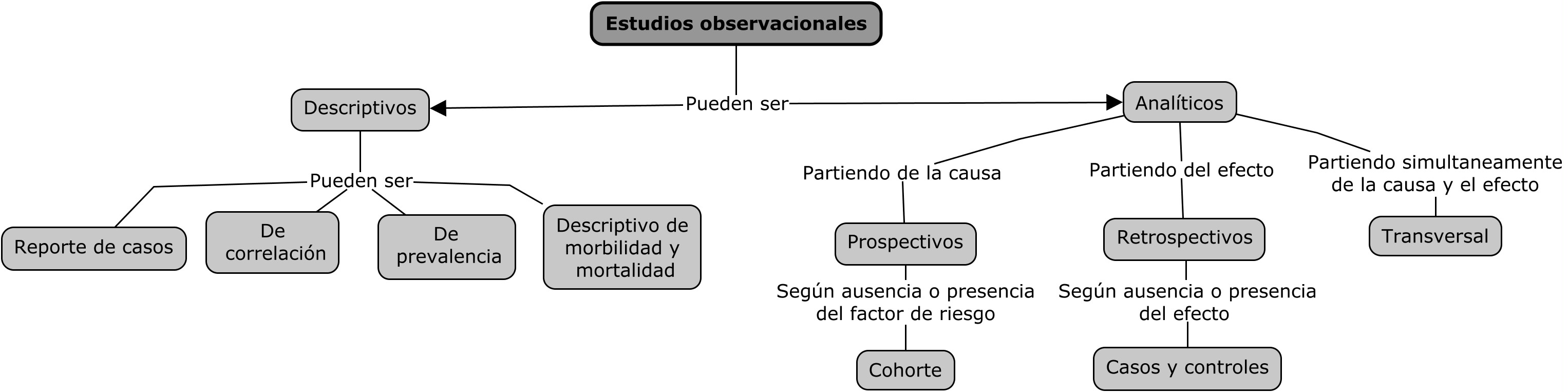
Los estudios observacionales suelen evaluarse mediante la creación de tablas de contingencia.
Una tabla de contingencia se asume como un arreglo bidimensional de f–filas por c–columnas. (Díaz Monroy and Morales Rivera 2009)
Se habla de una tabla de clasificación cruzada o tabla de contingencia cuando en una misma estructura se consideran dos variables categóricas con el objetiuvo de mostrar la relación que se presenta entre ellas. (Serna and Pareja 2017)

Para facilitar los cálculos y las interpretaciones de los estudios observacionales se aceptan unas convenciones en la estructura de las tablas de contingencia, las cuales son las siguientes:
Filas: Variable independiente.
Columnas: Variable dependiente.
Reporte de porcentajes por fila: Estudios transversales analíticos, estudios de cohortes y estudios experimentales.
Reporte de porcentajes por columnas: Estudios de casos y controles.
Reporte de porcentajes indistintamente: En caso que no se reconozca una variable dependiente y una independiente.
El tipo de tabla se nombra de acuerdo al número de filas y columnas que posea: Una tabla de 3 * 2 posee una variable independiente con 3 categorías (3 filas) y una variable dependiente con 2 categorías (2 columnas).
Las tablas más usadas son las de 2 * 2, estas tienen 4 celdas que se nombran por una letra siguiendo un orden por filas tal como se observa aquí abajo.
| Columna 1 | Columna 2 |
|---|---|
| a | b |
| c | d |
A continuación se muestra una guía rápida, útil para todo tipo de estudio epidemiológico, cada tipo de estudio puede requerir una modificación particular a esta guía general.
Identificar qué tipo de estudio es:
Empezar la descripción de lo más general a lo más específico, ejemplo:
Estudio observacional, analítico, retrospectivo de Casos y Controles.
Clasificar las variables de acuerdo a su interrelación:
Ejemplo:
En un estudio que busque analizar la asociación entre la condición corporal en cerdas al momento del parto y la presencia de metritis, debemos identificar qué variable es la independiente y cuál es la dependiente. Dado el planteamiento del estudio, la Condición Corporal es la variable independiente y la Metritis es la variable dependiente.
Clasificar las variables de acuerdo a su naturaleza:
Siguiendo el ejemplo anterior, clasificaremos las variables por su naturaleza.
Condición corporal (Gorda, Normal, Flaca): Variable cualitativa, ordinal, 3 categorías.
Metritis (presencia, ausencia): Variable cualitativa, nominal, dicotómica.
Esto será la base para la estructura de la tabla de contingencia, en este caso será una tabla de 3 * 2 (3 filas, 2 columnas).
Planteamiento de hipótesis: En estudios de Casos y Controles y en estudios de Cohorte se plantea una hipótesis nula y una hipótesis alternativa, en estudios transversales analíticos no.
Se debe plantear una Hipótesis nula (Ho) y una Hipótesis alternativa (Ha).
La Ho afirma que no hay asociación entre la variable independiente y la variable dependiente.
La Ha afirma que sí hay asociación entre la variable independiente y la variable dependiente.
Establecer un nivel de confianza: Aplica para los estudios donde se plantean hipótesis.
Generalmente los niveles de confianza son 99%, 95% o 90%.
Realizar la tabla de contingencia adecuada: Se realiza con base a las frecuencias observadas; es decir, con los conteos originales obtenidos.
Calcular las frecuencias relativas: Las frecuencias relativas se calculan obteniendo la proporción de cada celda respecto a su fila o columna dependiendo del tipo de estudio, en los estudios Transversales analíticos y en los estudios de Cohorte las frecuencias relativas se calculan obteniendio la proporción de cada celda respecto a su fila, mientras que en los estudios de Casos y Controles las frecuencias relativas se calculan obteniendio la proporción de cada celda respecto a su columna.
En R se puede usar el comando prop.table().
prop.table(x = tabla_de_frecuencias_observadas, margin = 1): Se usa margin = 1 en estudios Transversales analíticos y de Cohorte ya que indica que las proporciones se calcularán por filas.
prop.table(x = tabla_de_frecuencias_observadas, margin = 2): Se usa margin = 2 en estudios de Casos y Controles ya que indica que las proporciones se calcularán por filas.
Realizar gráficas: Las opciones más útiles son las gráficas de barras y las gráficas de mosaico.
Responder preguntas básicas:
En estudios Transversales analíticos es importante responder cuál es la prevalencia tanto en presencia como en ausencia del factor de riesgo.
En estudios de Casos y Controles es importante responder cuál es la prevalencia de la exposición en los diferentes niveles de la variable independiente.
En los estudios de Cohorte es importante responder cuál es la incidencia tanto en casos de presencia como en ausencia del factor de riesgo.
Calcular las frecuencias esperadas:
Se calculan para estudios de Casos y Controles y estudios de Cohorte

\[\begin{equation}{} Frecuencias\phantom{0}esperadas = \frac{\sum(f_i) . \sum(c_i)} {N} \end{equation}\]
Donde:
f = Fila
c = Columna
i = Celda a calcular (en una tabla de 2 X 2, i puede ser a, b, c, d)
N = Total de frecuencias
Decidir qué tipo de estadístico es el más adecuado: ji^2, Test exacto de Fisher, etc.
Rechazar o no la Ho: En estudios de Casos y Controles y estudios de Cohorte.
Medir la magnitud de la asociación: En estudios de Casos y Controles y estudios de Cohorte de haber signiicancia estadística (al rechazar Ho) se debe calcular el estadístico del tamaño del efecto adecuado.
En estudios Transversales no se realiza un test estadístico y tampoco se puede hablar de un tamaño del efecto y por tanto bastará con calcular la Razón de Prevalencia en caso de observar que la prevalencia no es la misma en los dos niveles de la variable independiente.
A continuación se muestran los estadísticos de la magnitud de la asociación según el tipo de estudio:
RP (Razón de Prevalencia) Para estudios transvetrsales analíticos.
OR (ODDS Ratio) Para estudios de Casos y Controles.
RR (Riesgo Relativo) Para estudios de Cohorte.
Estadísticos complementarios (Casos y Controles, y Cohorte): V de Cramer, Coeficiente Phi, Coeficiente de Contingencia.
Datos agrupados:
Si los datos ya están agrupados, la realización de la tabla de contingencia se puede hacer en R con el comando matrix.
Supongamos que nos dicen que tenemos 20 perros positivos a moquillo canino no vacunados y 15 vacunados, mientras que tenemos 30 perros negativos a moquillo canino no vacunados y 7 vacunados. Podemos hacer una tabla de 2 X 2 con estos datos:
matrix(data = c(20, 30, 15, 7), nrow = 2, ncol = 2, byrow = T) [,1] [,2]
[1,] 20 30
[2,] 15 7Explicación de la función matrix:
data: En ella se colocan las frecuencias, recomiendo colocar los datos en el orden de las celdas según la convención epidemiológica (primero la a, luego la b, después la c, y por último la d).
nrow = Indica cuántas filas tiene la matriz.
ncol = Indica cuántas columnas tiene la matriz.
byrow = Indica si los datos deben tomarse por filas o por columnas, dado que la recomendación es llenar los datos de acuerdo a la convención epidemiológica, entonces el comando byrow debe ser byrow = T
Podemos también agregar etiquetas para las columnas y filas con el comando dimnames, este comando acepta listas, por tanto usamos dimnanes = list(…), empezamos por los nombres de las filas c(…) y continuamos con las columnas c(…).
matrix(data = c(20, 30, 15, 7), nrow = 2, ncol = 2, byrow = T,
dimnames = list(
c("vacunados", "no vacunados"),
c("positivos", "negativos")
)
) positivos negativos
vacunados 20 30
no vacunados 15 7Datos sin agrupar:
Puede ser que los datos los obtengamos sin agrupar, y estén tabulados tal cuál se recabó la información, en tal caso los datos se podrían ver similares a estos
data.frame(
distemper = c(
"positivo", "positivo", "negativo", "negativo", "negativo"),
vacunacion = c(
"vacunado", "no vacunado", "vacunado", "no vacunado", "no vacunado")
) distemper vacunacion
1 positivo vacunado
2 positivo no vacunado
3 negativo vacunado
4 negativo no vacunado
5 negativo no vacunadoEs conveniente convertir las variables en factor para ordenarlas como deseamos (los positivos en la primera columna y los no vacunados en la primera fila)
# Guardamos nuestra tabla con el nombre datos_no_agrupados
datos_no_agrupados <- data.frame(
distemper = c(
"positivo", "positivo", "negativo", "negativo", "negativo"),
vacunacion = c(
"vacunado", "no vacunado", "vacunado", "no vacunado", "no vacunado")
)
# Procedemos a convertir las variables en factor
# En el comando levels colocamos el orden que deseamos
datos_no_agrupados$distemper <- factor(datos_no_agrupados$distemper,
levels = c("positivo", "negativo")
)
datos_no_agrupados$vacunacion <- factor(datos_no_agrupados$vacunacion,
levels = c("no vacunado", "vacunado")
)La tabla de contingencia la podemos crear con el comando table
table(datos_no_agrupados) vacunacion
distemper no vacunado vacunado
positivo 1 1
negativo 2 1Aquí surge el problema de que la variable independiente (vacunados, no vacunados) está en las columnas y la variable dependiente (distemper) en las filas, y según la convención epidemiológica la variable independiente debe ir en las filas y la dependiente en las columnas.
Entonces para solucionarlo podemos transponer los datos, esto se hace con el comando t(…)
t(table(datos_no_agrupados)) distemper
vacunacion positivo negativo
no vacunado 1 2
vacunado 1 1Se denomina estudio transversal porque la exposición y el resultado de la enfermedad se determinan simultáneamente para cada participante del estudio; es como si estuviéramos viendo una instantánea de la población en un momento determinado. (Celentano 2019)
A continuación se desarrollará un caso de ejemplo:
Se obtienen datos con el objetivo de encontrar una relación entre la presencia del virus de la Parainfluenza y la presencia de hacinamiento en perros sin raza definida de un refugio.
Para ello se toman muestras de perros con y sin hacinamiento y mediante una prueba de PCR se determina la presencia o ausencia del virus.
Dado que de manera simultanea se están evaluando los factores de la variable dependiente y los factores de la variable independiente, el tipo de estuido es Transversal analítico.
Variable dependiente: Parainfluenza
Variable independiente: Hacinamiento
Parainfluenza: Cualitativa, nominal, dicotómica.
Hacinamiento: Cualitativa, nominal, dicotómica.
Dado que tenemos una variable independiente con dos factores (sí, no) que irán en las filas, y una variable dependiente con dos factores (positivo, negativo) que irán en las columnas, la tabla de contingencia será de 2 X 2 (2 filas, 2 columnas).
La tabla que crearemos es una tabla de contingencia con las frecuencias absolutas observadas (es decir, las frecuencias originales obtenidas del estudio).
Crearemos una matriz con los datos
transversal <- matrix(data = c(5, 5, 1, 4), nrow = 2, ncol = 2, byrow = T,
dimnames = list(hacinamiento = c("si", "no"),
parainfluenza = c("presencia", "ausencia"))
)
transversal parainfluenza
hacinamiento presencia ausencia
si 5 5
no 1 4Con las frecuencias relativas se puede conocer la prevalencia de la enfermedad en los dos niveles de la variable independiente (celdas a y c), así también la falta de enfermedad en los dos niveles de la variable independiente (celdas b y d). El cálculo de las frecuencias relativas se hace por filas.
Cálculo manual
# Celda a
5 / (5 + 5)[1] 0.5# Celda b
5 / (5 + 5)[1] 0.5# Celda c
1 / (1 + 4)[1] 0.2# Celda d
4 / (1 + 4)[1] 0.8Atajo en R
Usamos el comando prop.table( ), es importante establecer en el argumento “margin” el valor “1” para que la sumatoria sea realizada por filas (el valor “2” hace la sumatoria por columnas).
# Creación de tabla de frecuencias relativas
(transversal_fr <- prop.table(transversal, margin = 1)) parainfluenza
hacinamiento presencia ausencia
si 0.5 0.5
no 0.2 0.8Gráficas
mosaicplot(transversal_fr, main = "Asociación Parainfluenza-Hacinamiento")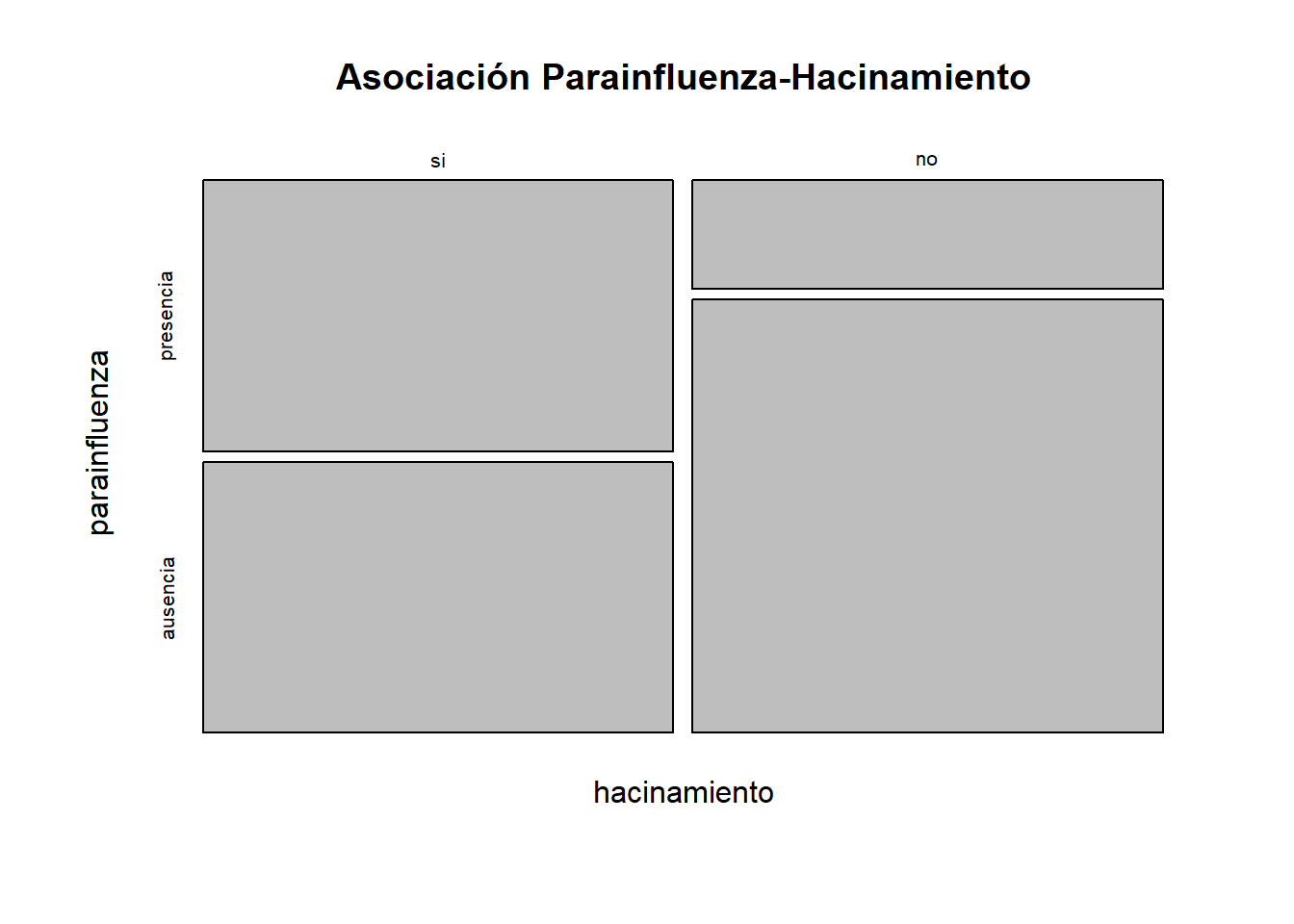
Gráficamente ya podemos observar que la prevalencia no es igual en los perros con hacinamiento que en los perros sin hacinamiento.
¿Cuál es la prevalencia de Parainfluenza en perros hacinados?
Basta con observar la frecuencia relativa de la celda "a"
50 %¿Cuál es la prevalencia de Parainfluenza en perros no hacinados?
Basta con observar la frecuencia relativa de la celda "c"
20 %Dado que la prevalencia con hacinamiento es diferente a la prevalencia sin hacinamiento, se realiza el cálculo de la magnitud de la asociación, la medida de la magnitud de la asociación en los estudios transversales analíticos es la Razón de Prevalencia (RP). Hablamos de magnitud de la asociación y no directamente del tamaño del efecto, porque dada la naturaleza del estudio no podemos saber si la variable independiente es la causante del efecto en la variable dependiente, ya que los perros positivos a Parainfluenza y que tuvieron hacinamiento pudieron contagiarse antes de estar en hacinamiento.

\[\begin{equation}{} RP = \frac {a / (a + b)} {c / (c + d)} \end{equation}\]
Realizando el cálculo “a mano” resulta
RP <- (5 / (5 + 5)) / (1 / (1 + 4))
RP[1] 2.5
Si RP = 1: No hay asociación.
Si RP > 1: El riesgo está aumentado.
Si RP < 1: El riesgo está disminuido.
Si a la RP le restamos 1, es decir
RP - 1[1] 1.5Dado que el resultado de RP - 1 es mayor que 1, podemos interpretar la respuesta como las veces que está aumentada la prevalencia de parainfluenza en condiciones de hacinamiento respecto a la prevalencia de parainfluenza en ausencia de hacinamiento.
Otra forma de interpretarlo es multiplicar por 100 el resultado de (RP - 1), es decir
(RP-1) * 100[1] 150Esto lo interpretamos como el % de aumento en la prevalencia de parainfluenza en presencia de hacinamiento, respecto a la prevalencia de parainfluenza en ausencia de hacinamiento.
Se emplean para determinar la asociación entre una enfermedad u otro evento de interés y factores de riesgo como condición pasada existente con el fin de aclarar su papel causal.
Para su realización, se seleccionan dos grupos de individuos tomando en cuenta la presencia de la enfermedad (casos) o la ausencia de la misma (controles).
El grupo de casos se conforma con individuos que presentan la enfermedad o evento de estudio; por ejemplo, perros con diagnóstico de cáncer de vejiga.
Por otra parte, el grupo de controles o testigos con individuos que no tienen la enfermedad o evento de estudio; por ejemplo, perros sanos o sin diagnóstico de cáncer de vejiga.
De cada uno de los individuos estudiados se obtiene información con respecto a su exposición a uno o más factores de riesgo o posibles factores de confusión en el pasado, de esta manera se hace la comparación entre la frecuencia de exposición al factor de riesgo de los casos y de los controles, para determinar la relación entre la exposición y la enfermedad o evento de interés, se deben examinar las historias de exposición en los casos y los controles. (Jaramillo Arango 2010)
A continuación se desarrollará un caso de ejemplo.
En una granja porcina, se observó en el último lote de gestación un aumento en el número de descargas vaginales mucopurulentas en hembras primerizas de 7 a 10 días postinseminación.
El veterinario revisó los registros y se percató que en algunas hembras se implementó inseminación postcervical mientras que en otras se utilizó inseminación tradicional.
Procedió a plantear un estudio para determinar si el tipo de inseminación está asociado a las descargas vaginales.
Para poder exponer este caso, crearemos una tabla con datos simulados para dos variables (descargas vaginales y métodos de inseminación), cada variable con dos factores o niveles.
La tabla será almacenada con el nombre “casos_controles” para facilitar su identificación.
# Tabla con los datos
casos_controles <- data.frame(
inseminacion = factor(#Se crea la variable como factor
c(rep("ipc", 18), rep("it", 7), rep("ipc", 6), rep("it", 10)),
levels = c("ipc", "it")#El 1er nivel siempre es el de interés
),
descargas = factor(#Se crea la variable como factor
c(rep("presencia", 25), rep("ausencia", 16)),
levels = c("presencia", "ausencia") #El 1er nivel siempre es el de interés
)
)
# Primeros 6 datos de la tabla
head(casos_controles) inseminacion descargas
1 ipc presencia
2 ipc presencia
3 ipc presencia
4 ipc presencia
5 ipc presencia
6 ipc presenciaDado que el estudio partió desde la causa hacia el efecto y se segregaron grupos con la afección y grupos sin la afección, esto nos indica que el estudio es de Casos y Controles.
Variable dependiente: Descargas vaginales.
Variable independiente: Método de inseminación.
Clasificar las variables de acuerdo a su naturaleza
Descargas vaginales (Presencia, Ausencia): Cualitativa, nominal, dicotómica.
Método de inseminación (Inseminación post cervical [IPC], Inseminación tradicional [IT]): Cualitativa, nominal, dicotómica.
Dado que tenemos una variable independiente con dos factores (ipc, it) que irán en las filas, y una variable dependiente con dos factores (presencia, ausencia) que irán en las columnas, la tabla de contingencia será de 2 X 2 (2 filas, 2 columnas).
La tabla que crearemos es una tabla de contingencia con las frecuencias absolutas observadas (es decir, las frecuencias originales obtenidas del estudio). Para ello usamos el comando “table”, dentro del paréntesis colocamos primero la variable independiente (filas) y luego la variable dependiente (columnas).
Usaremos el comando table( ), para crear la tabla como matriz ver el paso 4 del estudio Trasnversal Analítico.
(casos_controles_table <- table(casos_controles)) descargas
inseminacion presencia ausencia
ipc 18 6
it 7 10Con la frecuencia relativa se puede conocer la prevalencia de la enfermedad en presencia y en ausencia del factor de riesgo (celdas a y c), así también la falta de enfermedad en presencia y en ausencia del factor de riesgo (celdas b y d). En el caso de los estudios de Casos y Controles las frecuencias relativas se calculan por columna (es decir que la suma de cada columna debe resultar 100% si el cálculo es un % o 1 si usamos una escala de 0 a 1).
Cálculo manual
# Celda a
18 / (18 + 7)[1] 0.72# Celda b
6 / (6 + 10)[1] 0.375# Celda c
7 / (18 + 7)[1] 0.28# Celda d
10 / (6 + 10)[1] 0.625Atajo en R
Se usa el comando prop.table, dentro del paréntesis se coloca la tabla de frecuencias observadas (la que ya creamos con el comando “table” y que almacenamos con el nombre casos_controles_table), debemos especificar también dentro del paréntesis el argumento “margin = 2” (el 2 le indica a R que las proporciones deben calcularse por columnas, si quisiéramos por el contrario que las proporciones se calculen por filas simplemente omitimos el argumento “margin” o colocamos “margin = 1”)
Por defecto prop.table calcula las proporciones en una escala de 0 a 1.
prop.table(casos_controles_table, margin = 2) descargas
inseminacion presencia ausencia
ipc 0.720 0.375
it 0.280 0.625Si queremos que las proporciones sean porcentajes basta con multiplicar todo por 100
prop.table(casos_controles_table, margin = 2) * 100 descargas
inseminacion presencia ausencia
ipc 72.0 37.5
it 28.0 62.5plot(casos_controles_table, main = "Asociación Descargas-Inseminación")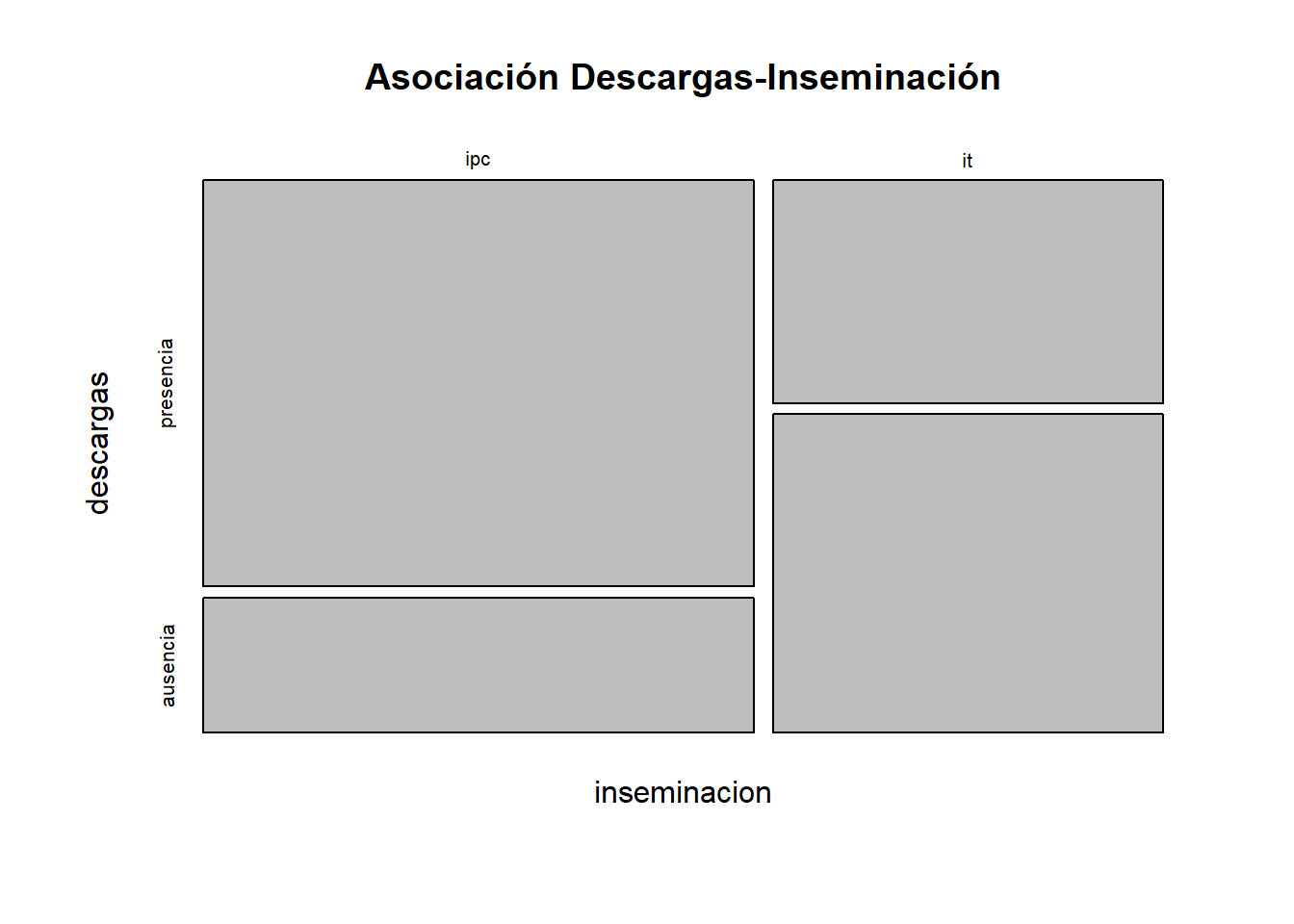
Calcular las frecuencias esperadas
Las frecuencias esperadas se calculan con base en las frecuencias observadas. Cada frecuencia esperada se corresponde con una frecuencia observada; por tanto, si tenemos 4 celdas de frecuencias observadas (a, b, c, d), se corresponderán 4 celdas de frecuencias esperadas (a_e, b_e, c_e, d_e).
Hay celdas que comparten la misma fila y celdas que comparten la misma columna; sin embargo, no hay celdas que compartan a la vez la misma fila y la misma columna; por tanto, cada celda tiene una combinación única de fila y columna; basado en esto, la frecuencia esperada de cada celda se calcula tomando la suma de su fila correspondiente y multiplicándola por la suma de su columna correspondiente, luego ese resultado de divide dentro del total de los datos.

\[\begin{equation}{} \frac{\sum(f_i) . \sum(c_i)} {\sum(f_i) + \sum(c_i)} \end{equation}\]
Donde:
f = Fila
c = Columna
i = Celda a calcular (en una tabla de 2 X 2, i será a, b, c, d)
A continuación se mostrará nuevamente la tabla de frecuencias observadas para que sirva de referencia y se entienda claramente el cálculo de las frecuencias esperadas:
#Frecuencias observadas, las cuales son la base
#para el cálculo de las frecuencias esperadas
casos_controles_table descargas
inseminacion presencia ausencia
ipc 18 6
it 7 10A continuación se muestra el cálculo de las frecuencias esperadas:
# Frecuencia esperada de la celda a
(a_e <- ((18 + 7) * (18 + 10)) / (18 + 7 + 10 + 15))[1] 14#Frecuencia esperada de la celda b
(b_e <- ((18 + 7) * (7 + 15)) / (18 + 7 + 10 + 15))[1] 11#Frecuencia esperada de la celda c
(c_e <- ((10 + 15) * (18 + 10)) / (18 + 7 + 10 + 15))[1] 14#Frecuencia esperada de la celda d
(d_e <- ((18 + 7) * (7 + 15)) / (18 + 7 + 10 + 15))[1] 11Ahora estas frecuencias se reunirán en una matriz, simplemente para visualizarlas mejor
#Creación de una matriz que contenga las celdas creadas y así se
#facilite su visualización
casos_controles_fe <- matrix(data = c(a_e, b_e, c_e, d_e),
nrow = 2, ncol = 2,
byrow = T
)
#Etiquetado de filas y columnas
dimnames(casos_controles_fe)[[1]] <- c("ipc", "it")
dimnames(casos_controles_fe)[[2]] <- c("presencia", "ausencia")
#Frecuencias esperadas
casos_controles_fe presencia ausencia
ipc 14 11
it 14 11Elegir el estadístico de asociación
Para elegil el estadístico adecuado se deben considerar algunos criterios:
Si al menos una variable es ordinal (o se observa tendencia): Ji cuadrado de linealidad.
Si no hay variables ordinales (ni tendencia) y más del 20% de las frecuencias esperadas son menores a 5: Test exacto de Fisher.
Si no hay variables ordinales (nio tendencia) y el 20% o menos de las frecuencias esperadas son menores a 5: Ji cuadrado de Pearson.
Dado que las variables son nominales (y sin tendencia aparente) y a que menos del 20% de las frecuencias esperadas son menores a 5, el estadístico adecuado es el ji2 de Pearson.
El contraste Chi-cuadrado es un procedimiento estadístico general para verificar el ajuste de un conjunto de datos a una hipótesis relativa a uan distribución, a la independencia de dos sucesos (Análisis de tablas de contingencia) o a la permanencia o consistencia de una hipótesis sobre distintas muestras de una población. (García 2012)
En este tipo de pruebas se deben plantear dos hipótesis, una hipótesis nula (Ho) y una hipótesis alterna (Ha).
La hipótesis nula que se ensaya siempre es: Ho) Las filas y columnas son independientes. (García 2012)
Así pues, la Ha sería que las filas y columnas no son independientes.
Dicho de otro modo podemos decir que Ho afirma que No hay asociación entre las variables y Ha afirma que Sí hay asociación entre las variables.

\[\begin{equation}{} X^2 = \sum^k_{i=1} \frac{ (O_i - E_i)^2} {E_i} \end{equation}\]
Si observamos la fórmula notaremos que se evalúa de alguna forma la magnitud entre las frecuencias observadas y las frecuencias esperadas. Esto tiene sentido si consideramos que (García 2012) indica que si el estadístico toma un valor excesivamente alto, significa que las frecuencias observadas son muy diferentes de las esperadas y la hipótesis nula debe rechazarse.
Cálculo manual:
Para hacer el cálculo manual observemos primero las frecuencias observadas y las frecuencias esperadas
Frecuencias observadas
# Frecuencias observadas
casos_controles_table descargas
inseminacion presencia ausencia
ipc 18 6
it 7 10Frecuencias esperadas
# Frecuencias esperadas
casos_controles_fe presencia ausencia
ipc 14 11
it 14 11Ahora sí, calculamos el estadístico de asociación
casos_controles_ji2 <-
((18 - 14)^2 / 14) +
((7 - 11)^2 / 11) +
((10 - 14)^2 / 14) +
((15 - 11)^2 / 11)
casos_controles_ji2[1] 5.194805Corrección de Yates
La corrección de Yates es un ajuste que se hace en la fórmula de ji2 en caso que la tabla de contingencia sea de 2 X 2, esto es debido a que en tablas de 2 X 2 los grados de libertad son 1 por tanto sin realizar ningún ajuste el estadístico tiende a sobreestimar la asociación entre las variables.

\[\begin{equation}{} X^2_{yates} = \sum^k_{i=1} \frac{ (|O_i - E_i| - 0.5)^2} {E_i} \end{equation}\]
#Corrección de Yates
casos_controles_yates <-
((abs(18 - 14) - 0.5)^2 / 14) +
((abs(7 - 11) - 0.5)^2 / 11) +
((abs(10 - 14) - 0.5)^2 / 14) +
((abs(15 - 11) - 0.5)^2 / 11)
casos_controles_yates[1] 3.977273Atajo en R: ji^2 sin corrección de yates y con corrección de yates
# Sin corrección
chisq.test(casos_controles_table)
Pearson's Chi-squared test with Yates' continuity correction
data: casos_controles_table
X-squared = 3.4685, df = 1, p-value = 0.06255#Con corrección
chisq.test(casos_controles_table, correct = T)
Pearson's Chi-squared test with Yates' continuity correction
data: casos_controles_table
X-squared = 3.4685, df = 1, p-value = 0.06255
Valor p < 0.05 = Significancia estadística (Asociación entre las variables).
Valor p >= 0.05 = No significancia estadística (No hay asociación entre las variables).
Sin corrección de Yates: Rechazamos la Ho con una confianza del 95% y concluimos que sí hay asociación entre las variables.
Con corrección de Yates: No rechazamos la Ho con una confianza del 95% y concluimos que no hay asociación entre las variables. Si la confianza la reducimos podríamos rechazar la Ho con una confianza del 90% y concluir que sí hay asociación entre las variables.
Una vez que se establece que sí hay asociación entre las variables se procede a calcular el estadístico del tamaño del efecto, el cuál para un estudio epidemiológico de Casos y Controles es el OR (ODDS Ratio).

\[\begin{equation}{} OR = \frac {a / c} {b/d} \end{equation}\]
Cálculo a mano
a <- casos_controles_table[1]
b <- casos_controles_table[3]
c <- casos_controles_table[2]
d <- casos_controles_table[4]
OR <- (a / c) /
(b / d)
OR[1] 4.285714Intervalos de confianza (IC) para el OR

\[\begin{equation}{} IC = exp[ ln(OR) ± (z{\alpha_{1/2}} · ee ) ] \end{equation}\]
Donde:
exp = Exponencial
ln = Logaritmo natural
\(z{\alpha_{1/2}}\) = Valor crítico de la distribucion normal estandar
\(ee (error\phantom{0} estandar) = \sqrt(1/a) + (1/b) + (1/c) + (1/d)\)
ln_OR <- log(OR)
za2 <- qnorm(1-(0.05/2))
ee <- sqrt((1/18) + (1/7) + (1/10) + (1/15))
# Intervalos de confianza
li <- exp(log(OR) - (za2 * ee))
ls <- exp(log(OR) + (za2 * ee))
# Límite inferior
li[1] 1.31133# Límite superior
ls[1] 14.00666
Si OR = 1: No hay asociación.
Si OR > 1: El riesgo está aumentado.
Si OR < 1: El riesgo está disminuido.
Si a la OR le restamos 1, es decir
OR - 1[1] 3.285714Esto lo interpretamos como las veces más de riesgo de presentar leptospirosis siendo macho que siendo hembra.
Otra forma de interpretarlo es multiplicar por 100 el resultado de (OR - 1), es decir
(OR-1) * 100[1] 328.5714Y esto lo interpretamos como el porcentaje de aumento de riesgo de presentar descargas vaginales al inseminar con el método postcervical comparada con el método tradicional.

\[\begin{equation}{} \phi = \frac{a · d - b · c} {\sqrt(a + b) · (c + d) · (a + c) · (b + d)} \end{equation}\]
O bien la siguiente
\[\begin{equation}{} \phi = \sqrt\frac{X^2} {N} \end{equation}\]
La utilización de una u otra fórmula puede variar ya que como se puede notar, la primera fórmula utiliza la tabla de contingencia tal cuál, es decir que se usan las frecuencias observadas; mientras que la segunda fórmula utiliza el resultado del Chi-cuadrado, así también el resultado puede variar si se utiliza el chi-2 con corrección o sin corrección de yates. Aquí se utilizará la segunda fórmula y se utilizará con corrección de yates.
chi2_yates_casos_controles <- chisq.test(casos_controles_table, correct = T)
sqrt(chi2_yates_casos_controles$statistic / sum(casos_controles_table))X-squared
0.2908558 Esto lo interpretamos como la proporción de la variable dependiente explicada por la variable independiente.
Se emplean para determinar el grado de asociación entre la exposición a un factor de riesgo y la subsecuente presentación de una enfermedad o muerte.
Para la realización de este tipo de estudios se seleccionan dos grupos de individuos con base en su relación al factor de exposición que se identifican como cohortes.
Una cohorte es un grupo de individuos sometidos a una misma experiencia (exposición a un factor de riesgo), que son seguidos de manera temporal desde la fecha de exposición a esa experiencia, que puede ser diferente de un individuo a otro, de tal manera que se van obteniendo datos sobre incidencia y exposición al factor de riesgo en todos los individuos estudiados, controlando todos los posibles sesgos y factores de confusión que pudieran afectar la interpretación de los resultados.
Para su diseño, se define primero el periodo de observación, el cual depende del tiempo que transcurre entre la exposición al factor de riesgo y la aparición del evento de estudio (periodo de incubación). Posteriormente, se identifica un grupo de individuos que al inicio del periodo de observación no se encuentren afectados por el evento de estudio, el cual puede estar constituido por la población estudiada o una muestra de la misma.
Una vez que en este grupo se determina su grado de exposición al factor de riesgo, ausencia del evento en estudio o de otros asociados y posibles factores de confusión, se conforman las dos cohortes. Cohorte expuesta: grupo de individuos sin el evento en estudio y expuestos al factor de riesgo en estudio; por ejemplo, granjas que no suministran calostro a los becerros dentro de las primeras seis horas de nacidos.
Cohorte no expuesta: grupo de individuos sin el evento en estudio y no expuestos al factor de riesgo en estudio; por ejemplo, granjas que suministran calostro a los becerros dentro de las primeras seis horas de nacidos.
Las cohortes así definidas tendrán seguimiento de manera sistemática durante el periodo de observación, para medir en ellas las variaciones en la exposición al factor de riesgo; pero principalmente para determinar la incidencia del evento en estudio, de tal manera que al finalizar dicho periodo es posible saber qué tanto difiere la incidencia del evento entre los expuestos y los no expuestos. (Jaramillo Arango 2010)
A continuación se desarrollará un caso de ejemplo.
En una finca de ganado vacuno se quiso evaluar la alimentación basada en alfalfa; sin embargo, sospechaban que inclusiones altas en la dieta podrían ocasionar timpanismo; por tanto, se decidió seleccionar animales libres de timpanismo y se formaron dos grupos: a uno se le proporcionó una dieta alta en alfalfa y a otro se le proporcionó una dieta baja en alfalfa.
Durante un mes se le dió seguimiento a ambos grupos y se fué registrando la incidencia de timpanismo.
De los 30 animales alimentados con altos niveles de alfalfa, 25 presentaron timpanismo y 5 no; de los 30 animales alimentados con niveles bajos de alfalfa, 16 presentaron timpanismo y 14 no.
Paso 1: Identificar el tipo de estudio
Dado que el estudio partió desde los factores de riesgo hacia adelante, el estudio es de Cohorte.
Clasificar las variables de acuerdo a su interrelación
Variable dependiente: Timpanismo.
Variable independiente: Niveles de alfalfa.
Clasificar las variables de acuerdo a su naturaleza
Timpanismo (Sí, No): Cualitativa, nominal, dicotómica.
Niveles de Alfalfa (Alto, Bajo): Cualitativa, nominal, dicotómica.
Formulación de hipótesis
Ho: No hay asociación entre la variable dependiente y la variable independiente
Ha: Sí hay asociación entre la variable dependiente y la variable independiente
Creación de tabla de contingencia de frecuencias observadas
Dado que tenemos una variable independiente con dos factores y una variable dependiente con dos factores, la tabla de contingencia será de 2 X 2 (2 filas, 2 columnas).
(cohorte <- matrix(c(25, 5, 16, 13), nrow = 2, ncol = 2, byrow = T,
dimnames = list(alfalfa = c("alto", "bajo"),
timpanismo = c("si", "no"))
)) timpanismo
alfalfa si no
alto 25 5
bajo 16 13prop.table(cohorte, margin = 1) timpanismo
alfalfa si no
alto 0.8333333 0.1666667
bajo 0.5517241 0.4482759Dado que no hay frecuencias espreadas menores a 5 se selecciona la prueba de Chi 2 de pearson y dado que la tabla es de 2 X 2 se usará la corrección de Yates.
chisq.test(cohorte, correct = T)
Pearson's Chi-squared test with Yates' continuity correction
data: cohorte
X-squared = 4.2675, df = 1, p-value = 0.03885Dado que el valor p es menor a la significancia, rechazamos Ho y concluimos que sí hay asociación entre la variable dependiente y la variable independiente con una confianza del 95%
Calcular el estimador del tamaño del efecto
En los estudios de Cohorte, el estimador del tamaño del efecto es el Riesgo Relativo (RR)

\[\begin{equation}{} RR = \frac {a / (a + b)} {c / (c + d)} \end{equation}\]
a <- cohorte[1]
b <- cohorte[3]
c <- cohorte[2]
d <- cohorte[4]
RR <-
(a / (a + b)) /
(c / (c + d))
RR[1] 1.510417Intervalos de confianza (IC) para el RR

\[\begin{equation}{} IC = exp[ ln(RR) ± (z{\alpha_{1/2}} · ee ) ] \end{equation}\]
Donde:
exp = Exponencial
ln = Logaritmo natural
\(z{\alpha_{1/2}}\) = Valor crítico de la distribucion normal estandar
\(ee (error\phantom{0} estandar) = \sqrt(1/a) + (1/b) + (1/c) + (1/d)\)
za2 <- qnorm(1-(0.05/2))
ee <- sqrt((1/a) + (1/b) + (1/c) + (1/d))
#Límite inferior
li <- exp(log(RR) - (za2 * ee))
li[1] 0.4516264#Límite superior
ls <- exp(log(RR) + (za2 * ee))
ls[1] 5.051428
Si RR = 1: El factor de riesgo no aumenta ni disminuye la probabilidad de enfermedad.
Si RR > 1: El riesgo está aumentado; es decir que, el factor de riesgo aumenta la probabilidad de enfermedad.
Si RR < 1: El riesgo está disminuido; es decir que, el factor de riesgo es un factor protector.
Si al RR le restamos 1, es decir
RR - 1[1] 0.5104167Esto lo interpretamos como las veces más de riesgo de presentar timpanismo consumiendo altos niveles de alfalfa en relación a un consumo bajo de alfalfa.
Otra forma de interpretarlo es multiplicar por 100 el resultado de (OR - 1), es decir
(RR - 1) * 100[1] 51.04167Esto lo interpretamos como el porcentaje de aumento de riesgo de presentar timpanismo con un consumo alto de alfalfa respecto a un consumo bajo de alfalfa.
\[\begin{equation}{} \phi = \frac{a · d - b · c} {\sqrt(a + b) · (c + d) · (a + c) · (b + d)} \end{equation}\]
o bien la siguiente
\[\begin{equation}{} \phi = \sqrt \frac{X^2} {N} \end{equation}\]
sqrt(chisq.test(cohorte, correct = T)$statistic / sum(cohorte))X-squared
0.2689425 Esto lo interpretamos como la proporción de la variable dependiente explicada por la variable independiente.